【文档说明】《道路勘测设计》7-3-2-平面设计课件.ppt，共(19)页，1.134 MB，由飞向未来上传

转载请保留链接：https://www.ichengzhen.cn/view-112536.html

以下为本文档部分文字说明：

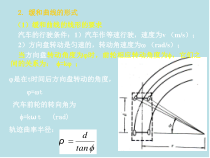
φ（1）缓和曲线的线形的要求汽车的行驶条件：1）汽车作等速行驶，速度为v（m/s）；2）方向盘转动是匀速的，转动角速度为（rad/s）；当方向盘转动角度为时，前轮相应转动角度为，它们之间的关系为：=k；2.缓和曲线的形式是在t时间后方向盘转动的角度，=t汽车前

轮的转向角为=kωt(rad)轨迹曲率半径：tandρ设汽车前后轮轴距为d，前轮转动后，汽车的行驶轨迹曲线半径为tkddtandρ汽车以v（m／s）等速行驶，经时间t以后，其行驶距离（弧长）为l：l=v

t(m)，ρωkdtρρ1.kvdkvdlωωkωvdCρCl汽车匀速从直线进入圆曲线（或相反）其行驶轨迹的弧长与曲线的曲率半径之乘积为一常数，这一性质与数学上的回旋线正好相符。Cl（

2）《标准》规定以回旋线作为缓和曲线。YX3.4.2缓和曲线的布设RLsAOLs1．回旋线的数学表达式我国现行《标准》规定缓和曲线采用回旋线。回旋线的基本公式表示为：ρ·l=C=A2式中：A——回旋线的参数缓和曲线起点：

回旋线的起点，l=0，r=∞；缓和曲线终点：回旋线某一点，l＝Ls，r＝R。则RLs=A2，即回旋线的参数值为：由微分方程推导回旋线的直角坐标方程：以ρl=A2代入得：回旋线微分方程为：dl=ρ·ddx=dl·cosdy=dl·sindβlAdl2

•1.回旋线的数学表达式：dAdll2cos2sin2AdxdAdyd0000cos2sin2AxdAyd2020()cos()2()sin()2xxCxtdtSytdt

00220220cos()2sin()2XAtdtYAtdtMatlab菲涅尔函数当l=0时，=0。对l·dl=A2·d积分得：式中：——回旋线上任一点的半径方向与Y轴的夹角。对回旋线微分方程组中的dx、dy积分时，

可把cos、sin用泰勒级数展开，然后用代入β表达式，再进行积分。22222,2AlAl!6!4!21cos!7!5!3sin642753cosdldxsindldydx，dy的展开：dldl·d

x)!6!4!21(cos642βdlAlAlAl])2(7201)2(241)2(21-1[622422222dlAlAlAl)6472038481(12128844dl(βdlβdy)!7!5!3sin753

dlAlAlAlAl])2(50401)2(1201)2(61-2[72252232222dlAlAlAlAl)12850403840482(14141010462245401Al对dx、dy分别进行积

分：dldxxcosdlAlAl)38481(88448945345640AlAlldldyysindlAlAlAl)3840482(1010462210116723422403366AlAlAl67

233366AlAl在回旋线终点处，l=Ls，r=R，A2=RLs回旋线终点坐标计算公式：8945345640ALsALsLsX10116723422403366ALsALsALsY56342422403366

RLsRLsRLs回旋线终点的半径方向与Y轴夹角β0计算公式：RLsALs222023R40LsLs4523345640RLsRLsLs3423366RLsRLs（1）切线角β。回旋线上任意点处的切线与回旋线起点或终点的切线（x轴）的交角,

被称作切线角。2.回旋线的几何要素22222A2lA2lρ在回旋线起点ZH或HZ点处，l=LS，该点的切线角表示为β0RLs20（2）内移值p：)1(cos00Ryp34s2sR2384LR24Lp（3）切线增值q：00sinR

xq232402RLLqssqtgpRTh2)(曲线长：LsRLsRLh1802180)2(0外距：Jh=2Th-Lh道路平面线形三要素的基本组成是：直线-回旋线-圆曲线-回旋线-直线。(1)曲线要素的计算公式：3．有缓和曲线的道路平曲线几何元素：切线长：RpR

Eh2sec)(校正值：(2)主点里程桩号计算方法：以交点里程桩号为起算点：ZH=JD–ThHY=ZH+LsQZ=ZH+Lh/2YH=HZ–LsHZ=ZH+LhJD=QZ+Jh/2①用切线支距法敷设回旋线公式：式中：l——回旋线上任

意点m至缓和曲线终点的弧长（m）。（3）切线支距法（直角坐标法）敷设曲线计算方法：225454040SLRllAllxSRLlAlAly6336636723x=q+Rsinm(m)y=p+R(1-cosm)(m)式中：)()2(6479.280RLslmm

δlm——圆曲线上任意点m至缓和曲线终点的弧长（m）；δ——lm所对应的圆心角（rad）。RlmδnβOMαnYHHYHZZHβδφyxqpRRsinφR(1-cosφ)00②切线支距法敷设带有回旋线的圆

曲线公式：例题：已知平原区某二级公路有一弯道，JD=K2+536.48，偏角α右=15°28′30″，半径R=600m，缓和曲线长度Ls=70m要求：（1）计算曲线主点里程桩号；（2）计算曲线上每隔25(10)m整桩号切线支距值。340.025024702422RL

sp996.342502407027024022323RLsLsq565.116996.3422830.15)340.0250(2)(tgqtgpRT054.232702502830.15180180

LsRL865.52502sec)340.0250(2sec)(RpREJ=2T-L=2×116.565-232.054=1.077解：（1）曲线要素计算：（2）主点里程桩号计算：以交点里程桩号为起算点：JD=K2+536.48ZH=JD–T=K2+536.48-11

6.565=K2+419.915HY=ZH+Ls=K2+419.915+70=K2+489.915QZ=ZH+L/2=K2+419.915+232.054/2=K2+535.942HZ=ZH+L=K2+419.915+232.054=K2+651.969

YH=HZ–Ls=K2+651.97–70=K2+581.969计算切线支距值：（1）LCZ=K2+425（缓和曲线段），ZH=K2+419.915l=2425-2419.915=5.085085.57025040085.5085

.5404012222545SLRllAlx000.0702506085.5663323SRLlAly（2）LCZ=K2+500，HY=K2+489.915（圆曲线段）lm=2500-2489.915=10.085x=q+Rsinm=34.996+2

50sin4.3053=80.038(m)y=p+R(1-cosm)=0.34+250（1-cos4.3053）=2.033(m)3053.4)25070085.102(9479.28

)2(6479.280RLslmmm（3）计算曲线上每隔25m整桩号的切线支距值：列表计算曲线25m整桩号：ZH=K2+419.915K2+425K2+450K2+475K2+500…作业：1．用级数展开法计算p、q的表达式。2．已知某一级公路（设计速度V=100Km/h），

有一弯道，偏角α左=16°36′42″，半径R=1000m，JD=K7+153.63。要求：（1）计算曲线主点里程桩号；（2）计算曲线上每隔25m整桩号的切线支距值（列表计算）。